python - How to trace the path in a Breadth-First Search?

Question

How do you trace the path of a Breadth-First Search, such that in the following example:

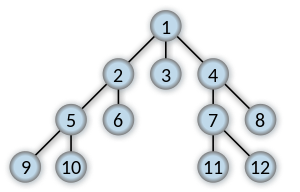
If searching for key 11, return the shortest list connecting 1 to 11.

[1, 4, 7, 11]

Answer 1

You should have look at http://en.wikipedia.org/wiki/Breadth-first_search first.

---

Below is a quick implementation, in which I used a list of list to represent the queue of paths.

# graph is in adjacent list representation
graph = {
        '1': ['2', '3', '4'],
        '2': ['5', '6'],
        '5': ['9', '10'],
        '4': ['7', '8'],
        '7': ['11', '12']
        }

def bfs(graph, start, end):
    # maintain a queue of paths
    queue = []
    # push the first path into the queue
    queue.append([start])
    while queue:
        # get the first path from the queue
        path = queue.pop(0)
        # get the last node from the path
        node = path[-1]
        # path found
        if node == end:
            return path
        # enumerate all adjacent nodes, construct a new path and push it into the queue
        for adjacent in graph.get(node, []):
            new_path = list(path)
            new_path.append(adjacent)
            queue.append(new_path)

print bfs(graph, '1', '11')

---

Another approach would be maintaining a mapping from each node to its parent, and when inspecting the adjacent node, record its parent. When the search is done, simply backtrace according the parent mapping.

graph = {
        '1': ['2', '3', '4'],
        '2': ['5', '6'],
        '5': ['9', '10'],
        '4': ['7', '8'],
        '7': ['11', '12']
        }

def backtrace(parent, start, end):
    path = [end]
    while path[-1] != start:
        path.append(parent[path[-1]])
    path.reverse()
    return path


def bfs(graph, start, end):
    parent = {}
    queue = []
    queue.append(start)
    while queue:
        node = queue.pop(0)
        if node == end:
            return backtrace(parent, start, end)
        for adjacent in graph.get(node, []):
            if node not in queue :
                parent[adjacent] = node # <<<<< record its parent 
                queue.append(adjacent)

print bfs(graph, '1', '11')

The above codes are based on the assumption that there's no cycles.

Answer 2

I liked qiao's first answer very much! The only thing missing here is to mark the vertexes as visited.

Why we need to do it?
Lets imagine that there is another node number 13 connected from node 11. Now our goal is to find node 13.
After a little bit of a run the queue will look like this:

[[1, 2, 6], [1, 3, 10], [1, 4, 7], [1, 4, 8], [1, 2, 5, 9], [1, 2, 5, 10]]

Note that there are TWO paths with node number 10 at the end.
Which means that the paths from node number 10 will be checked twice. In this case it doesn't look so bad because node number 10 doesn't have any children.. But it could be really bad (even here we will check that node twice for no reason..)
Node number 13 isn't in those paths so the program won't return before reaching to the second path with node number 10 at the end..And we will recheck it..

All we are missing is a set to mark the visited nodes and not to check them again..
This is qiao's code after the modification:

graph = {
    1: [2, 3, 4],
    2: [5, 6],
    3: [10],
    4: [7, 8],
    5: [9, 10],
    7: [11, 12],
    11: [13]
}


def bfs(graph_to_search, start, end):
    queue = [[start]]
    visited = set()

    while queue:
        # Gets the first path in the queue
        path = queue.pop(0)

        # Gets the last node in the path
        vertex = path[-1]

        # Checks if we got to the end
        if vertex == end:
            return path
        # We check if the current node is already in the visited nodes set in order not to recheck it
        elif vertex not in visited:
            # enumerate all adjacent nodes, construct a new path and push it into the queue
            for current_neighbour in graph_to_search.get(vertex, []):
                new_path = list(path)
                new_path.append(current_neighbour)
                queue.append(new_path)

            # Mark the vertex as visited
            visited.add(vertex)


print bfs(graph, 1, 13)

The output of the program will be:

[1, 4, 7, 11, 13]

Without the unneccecery rechecks..

Answer 3

Very easy code. You keep appending the path each time you discover a node.

graph = {
         'A': set(['B', 'C']),
         'B': set(['A', 'D', 'E']),
         'C': set(['A', 'F']),
         'D': set(['B']),
         'E': set(['B', 'F']),
         'F': set(['C', 'E'])
         }
def retunShortestPath(graph, start, end):

    queue = [(start,[start])]
    visited = set()

    while queue:
        vertex, path = queue.pop(0)
        visited.add(vertex)
        for node in graph[vertex]:
            if node == end:
                return path + [end]
            else:
                if node not in visited:
                    visited.add(node)
                    queue.append((node, path + [node]))

Answer 4

I thought I'd try code this up for fun:

graph = {
        '1': ['2', '3', '4'],
        '2': ['5', '6'],
        '5': ['9', '10'],
        '4': ['7', '8'],
        '7': ['11', '12']
        }

def bfs(graph, forefront, end):
    # assumes no cycles

    next_forefront = [(node, path + ',' + node) for i, path in forefront if i in graph for node in graph[i]]

    for node,path in next_forefront:
        if node==end:
            return path
    else:
        return bfs(graph,next_forefront,end)

print bfs(graph,[('1','1')],'11')

# >>>
# 1, 4, 7, 11

If you want cycles you could add this:

for i, j in for_front: # allow cycles, add this code
    if i in graph:
        del graph[i]

Answer 5

I like both @Qiao first answer and @Or's addition. For a sake of a little less processing I would like to add to Or's answer.

In @Or's answer keeping track of visited node is great. We can also allow the program to exit sooner that it currently is. At some point in the for loop the current_neighbour will have to be the end, and once that happens the shortest path is found and program can return.

I would modify the the method as follow, pay close attention to the for loop

graph = {
1: [2, 3, 4],
2: [5, 6],
3: [10],
4: [7, 8],
5: [9, 10],
7: [11, 12],
11: [13]
}


    def bfs(graph_to_search, start, end):
        queue = [[start]]
        visited = set()

    while queue:
        # Gets the first path in the queue
        path = queue.pop(0)

        # Gets the last node in the path
        vertex = path[-1]

        # Checks if we got to the end
        if vertex == end:
            return path
        # We check if the current node is already in the visited nodes set in order not to recheck it
        elif vertex not in visited:
            # enumerate all adjacent nodes, construct a new path and push it into the queue
            for current_neighbour in graph_to_search.get(vertex, []):
                new_path = list(path)
                new_path.append(current_neighbour)
                queue.append(new_path)

                #No need to visit other neighbour. Return at once
                if current_neighbour == end
                    return new_path;

            # Mark the vertex as visited
            visited.add(vertex)


print bfs(graph, 1, 13)

The output and everything else will be the same. However, the code will take less time to process. This is especially useful on larger graphs. I hope this helps someone in the future.

Answer 6

With cycles included in the graph, would not something like this work better?

from collections import deque

graph = {
    1: [2, 3, 4],
    2: [5, 6, 3],
    3: [10],
    4: [7, 8],
    5: [9, 10],
    7: [11, 12],
   11: [13]
}


def bfs1(graph_to_search, start, end):
    queue = deque([start])
    visited = {start}
    trace = {}

    while queue:
        # Gets the first path in the queue
        vertex = queue.popleft()
        # Checks if we got to the end
        if vertex == end:
            break

        for neighbour in graph_to_search.get(vertex, []):
            # We check if the current neighbour is already in the visited nodes set in order not to re-add it
            if neighbour not in visited:
            # Mark the vertex as visited
                visited.add(neighbour)
                trace[neighbour] = vertex
                queue.append(neighbour)

path = [end]
while path[-1] != start:
    last_node = path[-1]
    next_node = trace[last_node]
    path.append(next_node)

return path[::-1]

print(bfs1(graph,1, 13))

This way only new nodes will be visited and moreover, avoid cycles.