Since 'XYZ_Acc' is defined as a linear combination of the components of the signal, taking its DFT makes sense. It is equivalent to using a 1D accelometer in direction (1,1,1). But a more physical energy-related viewpoint can be adopted.
Computing the DFT is similar to writing the signal as a sum of sines. If the acceleration vector writes :
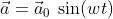
The corresponding velocity vector could write:
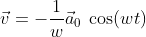
and the specific kinetic energy writes:
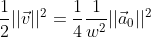
This method requires computing the DFT a each component before the magnitude corresponding to each frequency.
Another issue is that the DFT is intended to compute the Discrete Fourrier Transform of a periodic signal, that signal being build by periodizing the frame. Nevertheless, the actual frame is never a period of a periodic signal and repeating the period creates artificial discontinuities at the end/begin of the frame. The effects strong discontinuities in the spectral domain, deemded spectral leakage, could be reduced by windowing the frame. Computing the real-to-complex DFT result in a power distribution, featuring peaks at particular frequencies.
In addition the frequency of a given peak is better estimated as the mean frequency with respect to power density, as shown in Why are frequency values rounded in signal using FFT?
Another tool to estimate fundamental frequencies is to compute the autocorrelation of the signal: it is higher near the periods of the signal. Since the signal is a vector of 3 components, an autocorelation matrix can be built. It is a 3x3 Hermitian matrix for each time and therefore features real eigenvalues. The maxima of the higher eigen value can be picture as the magnitude of vaibrations while the correponding eigenvector is a complex direction, somewhat similar to the direction of vibrations combined to angular offsets. The angular offset may signal an ellipsoidal vibration.
Here is a fake signal, build by adding a guassian noise and sine waves:

Here is the power density spectrum for a given frame overlapping on sine wave:

Here is the resulting eigenvalues of the autocorrelation of the same frame, where the period of the 50Hz sine wave is visible. Vertical scaling is wrong:

Here goes a sample code:
import matplotlib.pyplot as plt
import numpy as np
import scipy.signal
n=2000
t=np.linspace(0.,n/200,num=n,endpoint=False)
# an artificial signal, just for tests
ax=0.3*np.random.normal(0,1.,n)
ay=0.3*np.random.normal(0,1.,n)
az=0.3*np.random.normal(0,1.,n)
ay[633:733]=ay[633:733]+np.sin(2*np.pi*30*t[633:733])
az[433:533]=az[433:533]+np.sin(2*np.pi*50*t[433:533])
#ax=np.sin(2*np.pi*10*t)
#ay=np.sin(2*np.pi*30*t)
#az=np.sin(2*np.pi*50*t)
plt.plot(t,ax, label='x')
plt.plot(t,ay, label='y')
plt.plot(t,az, label='z')
plt.xlabel('t, s')
plt.ylabel('acc, m.s^-2')
plt.legend()
plt.show()
#splitting the sgnal into frames of 0.5s
noiseheight=0.
for i in range(2*(n/200)):
print 'frame', i,' time ', i*0.5, ' s'
framea=np.zeros((100,3))
framea[:,0]=ax[i*100:i*100+100]
framea[:,1]=ay[i*100:i*100+100]
framea[:,2]=az[i*100:i*100+100]
#for that frame, apply window. Factor 2 so that average remains 1.
window = np.hanning(100)
framea[:,0]=framea[:,0]*window*2
framea[:,1]=framea[:,1]*window*2
framea[:,2]=framea[:,2]*window*2
#DFT transform.
hatacc=np.fft.rfft(framea,axis=0, norm=None)
# scaling by length of frame.
hatacc=hatacc/100.
#computing the magnitude : all non-zero frequency are doubled to merge energy in bin N-k exp(-2ik/n) to bin k
accmag=2*(np.abs(hatacc[:,0])*np.abs(hatacc[:,0])+np.abs(hatacc[:,1])*np.abs(hatacc[:,1])+np.abs(hatacc[:,2])*np.abs(hatacc[:,2]))
accmag[0]=accmag[0]*0.5
#first frame says something about noise
if i==0:
noiseheight=2.*np.max(accmag)
if np.max(accmag)>noiseheight:
peaks, peaksdat=scipy.signal.find_peaks(accmag, height=noiseheight)
timestep=0.005
freq= np.fft.fftfreq(100, d=timestep)
#see https://stackguides.com/questions/54714169/why-are-frequency-values-rounded-in-signal-using-fft/54775867#54775867
# frequencies of peaks are better estimated as mean frequency of peak, with respect to power density
for ind in peaks:
totalweight=accmag[ind-2]+accmag[ind-1]+accmag[ind]+accmag[ind+1]+accmag[ind+2]
totalweightedfreq=accmag[ind-2]*freq[ind-2]+accmag[ind-1]*freq[ind-1]+accmag[ind]*freq[ind]+accmag[ind+1]*freq[ind+1]+accmag[ind+2]*freq[ind+2]
print 'found peak at frequency' , totalweightedfreq/totalweight, ' of height', accmag[ind]
#ploting
plt.plot(freq[0:50],accmag[0:50], label='||acc||^2')
plt.xlabel('frequency, Hz')
plt.ylabel('||acc||^2, m^2.s^-4')
plt.legend()
plt.show()
#another approach to find fundamental frequencies: computing the autocorrelation of the windowed signal and searching for maximums.
#building the autocorellation matrix
autocorr=np.zeros((100,3,3), dtype=complex)
acxfft=np.fft.fft(framea[:,0],axis=0, norm=None)
acyfft=np.fft.fft(framea[:,1],axis=0, norm=None)
aczfft=np.fft.fft(framea[:,2],axis=0, norm=None)
acxfft[0]=0.
acyfft[0]=0.
aczfft[0]=0.
autocorr[:,0,0]=np.fft.ifft(acxfft*np.conj(acxfft),axis=0, norm=None)
autocorr[:,0,1]=np.fft.ifft(acxfft*np.conj(acyfft),axis=0, norm=None)
autocorr[:,0,2]=np.fft.ifft(acxfft*np.conj(aczfft),axis=0, norm=None)
autocorr[:,1,0]=np.fft.ifft(acyfft*np.conj(acxfft),axis=0, norm=None)
autocorr[:,1,1]=np.fft.ifft(acyfft*np.conj(acyfft),axis=0, norm=None)
autocorr[:,1,2]=np.fft.ifft(acyfft*np.conj(aczfft),axis=0, norm=None)
autocorr[:,2,0]=np.fft.ifft(aczfft*np.conj(acxfft),axis=0, norm=None)
autocorr[:,2,1]=np.fft.ifft(aczfft*np.conj(acyfft),axis=0, norm=None)
autocorr[:,2,2]=np.fft.ifft(aczfft*np.conj(aczfft),axis=0, norm=None)
# at a given time, the 3x3 matrix autocorr is Hermitian.
#Its eigenvalues are real, its unitary eigenvectors signals directions of vibrations and phase between components.
autocorreigval=np.zeros((100,3))
autocorreigvec=np.zeros((100,3,3), dtype=complex)
for j in range(100):
autocorreigval[j,:], autocorreigvec[j,:,:]=np.linalg.eigh(autocorr[j,:,:],UPLO='L')
peaks, peaksdat=scipy.signal.find_peaks(autocorreigval[:50,2], 0.3*autocorreigval[0,2])
cleared=np.zeros(len(peaks))
peakperiod=np.zeros(len(peaks))
for j in range(len(peaks)):
totalweight=autocorreigval[peaks[j]-1,2]+autocorreigval[peaks[j],2]+autocorreigval[peaks[j]+1,2]
totalweightedperiod=0.005*(autocorreigval[peaks[j]-1,2]*(peaks[j]-1)+autocorreigval[peaks[j],2]*(peaks[j])+autocorreigval[peaks[j]+1,2]*(peaks[j]+1))
peakperiod[j]=totalweightedperiod/totalweight
#cleared[0]=1.
fundfreq=1
for j in range(len(peaks)):
if cleared[j]==0:
print "found fundamental frequency :", 1.0/(peakperiod[j]), 'eigenvalue', autocorreigval[peaks[j],2],' dir vibration ', autocorreigvec[peaks[j],:,2]
for k in range(j,len(peaks),1):
mm=np.zeros(1)
np.floor_divide(peakperiod[k],peakperiod[j],out=mm)
if ( np.abs(peakperiod[k]-peakperiod[j]*mm[0])< 0.2*peakperiod[j] or np.abs(peakperiod[k]-(peakperiod[j])*(mm[0]+1))< 0.2*peakperiod[j]) :
cleared[k]=fundfreq
#else :
# print k,j,mm[0]
# print peakperiod[k], peakperiod[j]*mm[0], peakperiod[j]*(mm[0]+1) , peakperiod[j]
fundfreq=fundfreq+1
plt.plot(t[i*100:i*100+100],autocorreigval[:,2], label='autocorrelation, large eigenvalue')
plt.plot(t[i*100:i*100+100],autocorreigval[:,1], label='autocorrelation, medium eigenvalue')
plt.plot(t[i*100:i*100+100],autocorreigval[:,0], label='autocorrelation, small eigenvalue')
plt.xlabel('t, s')
plt.ylabel('acc^2, m^2.s^-4')
plt.legend()
plt.show()
The output is:
frame 0 time 0.0 s
frame 1 time 0.5 s
frame 2 time 1.0 s
frame 3 time 1.5 s
frame 4 time 2.0 s
found peak at frequency 50.11249238149811 of height 0.2437842149351196
found fundamental frequency : 50.31467771196368 eigenvalue 47.03344783764712 dir vibration [-0.11441502+0.00000000e+00j 0.0216911 +2.98101624e-18j
-0.9931962 -5.95276353e-17j]
frame 5 time 2.5 s
frame 6 time 3.0 s
found peak at frequency 30.027895460975156 of height 0.3252387031089667
found fundamental frequency : 29.60690406120401 eigenvalue 61.51059682797539 dir vibration [ 0.11384195+0.00000000e+00j -0.98335779-4.34688198e-17j
-0.14158908+3.87566125e-18j]
frame 7 time 3.5 s
found peak at frequency 26.39622018109896 of height 0.042081187689137545
found fundamental frequency : 67.65844834016518 eigenvalue 6.875616417422696 dir vibration [0.8102307 +0.00000000e+00j 0.32697001-8.83058693e-18j
0.48643275-4.76094302e-17j]
frame 8 time 4.0 s
frame 9 time 4.5 s
Frequencies 50Hz and 30Hz got caught as 50.11/50.31Hz and 30.02/29.60Hz and directions are quite accurate as well. The last feature at 26.39Hz/67.65Hz is likely garbage, as it features different frequencies for the two methods and lower magnitude/eigenvalue.
Regarding monitoring of road surface to improve maintenance, I know of a project at my compagny, called Aigle3D. A laser fitted at the back of a van scans the road at highway speed at milimetric accuracy. The van is also fitted with a server, cameras and other sensors, thus providing a huge amount of data on road geometry and defects, presently covering hundreds of km of the french national road network. Detecting and repairing small early defects and cracks may extend the life expectancy of the road at limited cost. If useful, data from accelerometers of daily users could indeed complete the monitoring system, allowing a faster reaction whenether a large pothole appears.






axis=1(1 corresponding to the dimension of time in the multidimensionnal array). Then the energy corresponding to each frequency can be computed by summing the square of components X, Y and Z. – francis