C++ Eigen for solving linear systems fast

Question

So I wanted to test the speed of C++ vs Matlab for solving a linear system of equations. For this purpose I create a random system and measure the time required to solve it using Eigen on Visual Studio:

#include <Eigen/Core>
#include <Eigen/Dense>
#include <chrono>

using namespace Eigen;
using namespace std;

int main()
{
    chrono::steady_clock sc;   // create an object of `steady_clock` class
    int n;
    n = 5000;
    MatrixXf m = MatrixXf::Random(n, n);
    VectorXf b = VectorXf::Random(n);
    auto start = sc.now();     // start timer
    VectorXf x = m.lu().solve(b);
    auto end = sc.now();
    // measure time span between start & end
    auto time_span = static_cast<chrono::duration<double>>(end - start);
    cout << "Operation took: " << time_span.count() << " seconds !!!";
}

Solving this 5000 x 5000 system takes 6.4 seconds on average. Doing the same in Matlab takes 0.9 seconds. The matlab code is as follows:

a = rand(5000);  b = rand(5000,1);

tic
x = a\b;
toc

According to this flowchart of the backslash operator:

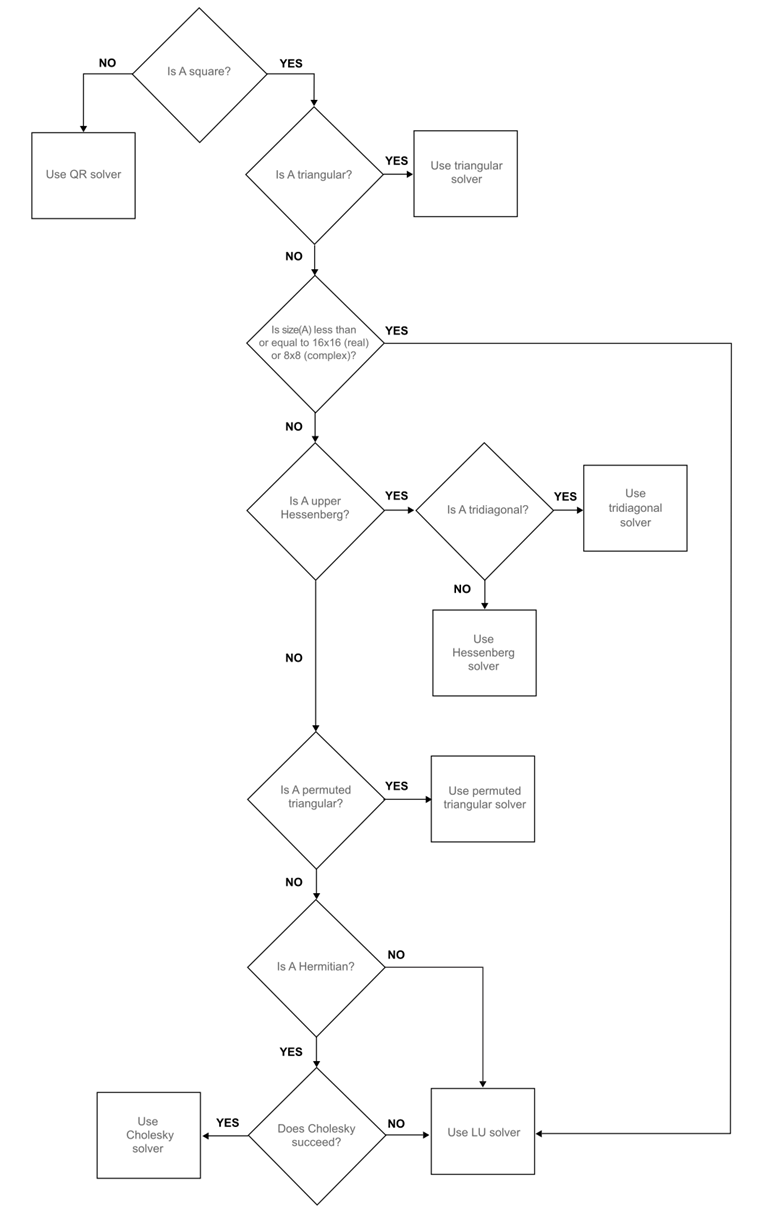
given that a random matrix is not triangular, permuted triangular, hermitian or upper heisenberg, the backslash operator in Matlab uses a LU solver, which I believe is the same solver that I'm using on the C++ code, that is, lu().solve

Probably there is something that I'm missing, because I thought C++ was faster.

I am running it with release mode active on the Configuration Manager
Project Properties - C/C++ - Optimization - /O2 is active
Tried using Enhanced Instructions (SSE and SSE2). SSE actually made it slower and SSE2 barely made any difference.
I am using Community version of Visual Studio, if that makes any difference

When I run your code on my machine, it takes 3.18 sec with -O3. I changed m.lu().solve(b); to m.llt().solve(b); and now it takes 0.1sec. — lakshayg
To be fair, isn't Matlab using double-precision by default, whereas your matrices are single precision? You might want to replace MatrixXf by MatrixXd and VectorXf by VectorXd, right? — Rulle
@Lakshay Garg If I'm not mistaken, llt().solve() uses the Cholesky decomposition LL' to solve the linear system, which should only be valid if the system matrix "m" is positive definite. Given that the matrix is random, this doesn't seem valid. — user3199900
Are you building 32-bit code? If so, why? 64-bit mode has twice as many SIMD registers available, and SSE2 is already the baseline. — Peter Cordes

ggael ggael · Accepted Answer · 2018-11-11T13:15:03

First of all, for this kind of operations Eigen is very unlikely to beat MatLab because the later will directly call Intel's MKL which is heavily optimized and multi-threaded. Note that you can also configure Eigen to fallback to MKL, see how. If you do so, you'll end up with similar performance.

Nonetheless, 6.4s is way to much. The Eigen's documentation reports 0.7s for factorizing a 4k x 4k matrix. Running your example on my computer (Haswell laptop @2.6GHz) I got 1.6s (clang 7, -O3 -march=native), and 1s with multithreading enabled (-fopenmp). So make sure you enable all your CPU's feature (AVX, FMA) and openmp. With OpenMP you might need to explicitly reduce the number of openmp threads to the number of physical cores.

C++ Eigen for solving linear systems fast

1 Answers