How to determine if a Delaunay triangle is internal or external?

Question

I am writing a program that requires a implementation of Medial Axis extraction, of which Delaunay triangulation is a step. External medial axis is unwanted so the corresponding external triangles are intended to be removed. Luckily I came upon a page with a lot of diagrams, also a hint of a method to determine internal and external Delaunay triangles ("based on the broken line perimeter"), but it's just a hint, without detailed explanation. Anybody know the algorithm?

EDIT: I forgot mentioning the initial points are sampled from the boundary of a closed polygon, my intention is to determine whether each Delaunay triangle is inside the polygon.

Answer 1

This solution assumes that you have a data structure that represents the Delaunay triangulation using a "virtual infinite Delaunay vertex" the way CGAL does it (see details here).

The idea is to find the boundary Delaunay edges: the edges connecting two consecutive sample points; and then "flood" through the Delaunay triangulation to classify the Delaunay faces. One knows that the infinite vertex is exterior so one can classify its neighbors (and neighbors' neighbors, etc.) as exterior as long as one does not cross boundary edges. If one reaches a boundary edge one can simply mark the neighbor triangle as interior and continue similarly.

Input: set of points densely sampling of the boundary of a closed shape, which can even contain holes
Output: Voronoi diagram in the interior of the shape (approximation of the medial axis of the shape)

1. Compute the Delaunay triangulation of your points
2. Mark the Delaunay edges which connect two consecutive sample points. (See page 4-5 of this paper how you can do this with a local test on every Delaunay edge)
3. Classify all infinite Delaunay faces as OUTSIDE and push them to a queue Q.
4. While Q is not empty
   1. Delaunay face f = Pop from Q
   2. For every unclassified neighbor triangle t of f
      • if the Delaunay edge shared by t and f is marked, classify t as the opposite of f
      • else classify t the same like f
      • push t to Q
5. For every Delaunay edge e
   • if the two neighbor Delaunay triangles d1, d2 are both classified as INTERIOR, output the segment connecting the circumcenter of d1 and d2.

For an input like this

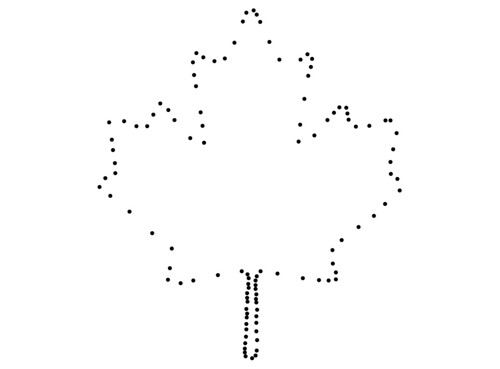
the following medial axis approximation can be computed:

You can check out how this medial axis approximation behaves in practice using the free windows binary of Mesecina. Source code here.

Answer 2

Have you considered using a different form of triangulation that doesn't create external triangles? I once took a course that spent a great deal of time discussing the theoretical aspects of polygon triangulation. Maybe skimming through the course site will give you some insight? http://cgm.cs.mcgill.ca/~godfried/teaching/cg-web.html#triangulation

Edit: Actually, I just thought of something else. If you already have the polygon that you are trying to triangulate, you could use Green's theorem. Green's theorem uses a polygon's perimeter to compute its area! More importantly, in this case, you can determine whether a point is on one side of a line, or another, by looking at the sign of area. On polygons, Green's theorem works out to a simple subtraction problem. So take any point that you KNOW is inside the polygon, and compute the area against each edge of the polygon. This tells you on which side of each line your point needs to be. Now simply take a point inside each triangle and do the same thing. If any of the signs are wrong, then you have an external triangle. (Note: depending on the shape of your polygon this might not actually work. It should work fine for convex polygons, but concavities could introduce additional complications.)

Answer 3

Perhaps I'm making too many assumptions here, but it sounds like you have a polygon that consists of a bunch of points, and that you are triangulating those points. You then want to discard all the triangles that fall outside of the polygon, right?

Why not just triangulate the polygon (using monotone decomposition or something similar) so that you never create any external triangles? I suppose this might increase the running time (triangulate first in O(nlogn) time and then create a delaunay triangulation in O(n^2) time) but there might be a faster way of doing it.

Answer 4

The algorithm that they present looks like it is a bit broken, as they show in one of their figures, and this may be the reason that there don't appear to be any useful citations in Google Scholar.

Using their proposed algorithm on a non-convex polygon shows that it does not always recover an actual triangulation. http://www.cc.kyoto-su.ac.jp/~atsushi/Jun/Topics/Teddy/images/example2_2.jpg