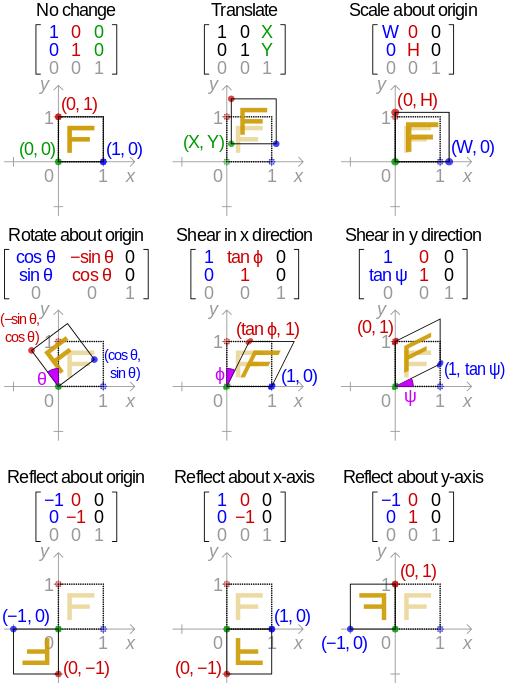
How is a transformation matrix defined?
I have the values defining scale, skew, and translation. I would like to find the transformation matrix they represent.
- Scale x/y can be any number.
- Translation x/y can be any number.
- Skew x/y is in degrees between -180 and 180.
How can I find the transformation matrix for these values?
I am working with values from Flash, and would like the matrix to be formatted like this, so that I can export this matrix and apply the same transformation in another language :
| a c u |
| b d v |
| 0 0 1 |
I need to be able to go from the parameters to the matrix outside of AS3/JSFL/Flash.
(Specifically I want to use C#, but I want an answer that doesn't depend on a given language.)
This link talks about how matrices work in Flash, and I understand most of it. However from what I can tell, it does not describe how to go from position/scale/skew values to a matrix. http://www.senocular.com/flash/tutorials/transformmatrix/
I know there is a .matrix property of flash display objects, but I am working with the given values outside of flash, and need to find a solution without using that.
Actionscript's skew is misbehaving
Given the usual definitions of tranformations in Cimbali's answer, I'm still having problems with building a matrix from its skew parameter.
Here is an example set of data:
A) Object Properties (logged directly from Flash using JSFL, element.x, element.skewX, etc...)
x: 0
y: 0
scaleX: 1
scaleY: 1.0000152587890625
skewX: 19.9998779296875
skewY: 0
B) Transform Matrix (logged directly from Flash using JSFL, element.matrix)
1 | 0 | 0
-0.342 | 0.94 | 0
0 | 0 | 1
Here is what I tried:
sx = tan(19.9998779296875 * PI / 180) = tan(0.34906372) = 0.36396782164
Scale Matrix Skew X Matrix Result Matrix
1 | 0 | 0 1 | 0 | 0 1 | 0 | 0
0 | 1 | 0 x 0.36 | 1 | 0 = 0.36 | 1 | 0
0 | 0 | 1 0 | 0 | 0 0 | 0 | 1
SkewY is 0, so there's no reason to multiply again using a Skew Y Matrix.
So why is my Result Matrix so much different than the matrix posted by Flash?
In this example my graphic is originally 200 x 100 px. It does not inherit transformations from any parent (the parent is definitely not transformed in any way). However, when I place the graphic on the stage and ONLY change the skew X value to 20°, the Height in the properties panel changes from100 to 94px, but Scale Y stays at 100%.
In case you're not familiar with Flash IDE, when you adjust ONLY the skew X value, it does not simply push the corners of the graphic left/right. It actually makes the corners move on an arc, as you increase skew X, the parallelogram comes shorter vertically.
(I realize I have rounded some numbers, but that is only for ease of displaying them here.)
tan(-19.99...)). The matrix JSFL spits out seems incorrect, or at least seems to be the "concatenation" of your matrix with one that is scaling the Y axis by 0.94 (0.36396782164 * 0.94 = 0.342and1*0.94 = 0.94). Is there a container, parent element, or anything at all that might explain this supplementary scaling ? Is it the same on other examples ? – Cimbalicos(0.34906372) = 0.9396so it seems to fit. I will update my answer. – Cimbali