I'm going to write a program where the input is a data set of 2D points and the output is the regression coefficients of the line of best fit by minimizing the minimum MSE error.
I have some sample points that I would like to process:
X Y
1.00 1.00
2.00 2.00
3.00 1.30
4.00 3.75
5.00 2.25
How would I do this in MATLAB?
Specifically, I need to get the following formula:
y = A + Bx + e
A is the intercept and B is the slope while e is the residual error per point.
Judging from the link you provided, and my understanding of your problem, you want to calculate the line of best fit for a set of data points. You also want to do this from first principles. This will require some basic Calculus as well as some linear algebra for solving a 2 x 2 system of equations. If you recall from linear regression theory, we wish to find the best slope m and intercept b such that for a set of points ([x_1,y_1], [x_2,y_2], ..., [x_n,y_n]) (that is, we have n data points), we want to minimize the sum of squared residuals between this line and the data points.
In other words, we wish to minimize the cost function F(m,b,x,y):
m and b are our slope and intercept for this best fit line, while x and y are a vector of x and y co-ordinates that form our data set.
This function is convex, so there is an optimal minimum that we can determine. The minimum can be determined by finding the derivative with respect to each parameter, and setting these equal to 0. We then solve for m and b. The intuition behind this is that we are simultaneously finding m and b such that the cost function is jointly minimized by these two parameters. In other words:
OK, so let's find the first quantity 
:
We can drop the factor 2 from the derivative as the other side of the equation is equal to 0, and we can also do some distribution of terms by multiplying the -x_i term throughout:
Next, let's tackle the next parameter 
:
We can again drop the factor of 2 and distribute the -1 throughout the expression:
Knowing that 
is simply n, we can simplify the above to:
Now, we need to simultaneously solve for m and b with the above two equations. This will jointly minimize the cost function which finds the best line of fit for our data points.
Doing some re-arranging, we can isolate m and b on one side of the equations and the rest on the other sides:
As you can see, we can formulate this into a 2 x 2 system of equations to solve for m and b. Specifically, let's re-arrange the two equations above so that it's in matrix form:
With regards to above, we can decompose the problem by solving a linear system: Ax = b. All you have to do is solve for x, which is x = A^{-1}*b. To find the inverse of a 2 x 2 system, given the matrix:
The inverse is simply:
Therefore, by substituting our quantities into the above equation, we solve for m and b in matrix form, and it simplifies to this:
Carrying out this multiplication and solving for m and b individually, this gives:
As such, to find the best slope and intercept to best fit your data, you need to calculate m and b using the above equations.
Given your data specified in the link in your comments, we can do this quite easily:
%// Define points
X = 1:5;
Y = [1 2 1.3 3.75 2.25];
%// Get total number of points
n = numel(X);
% // Define relevant quantities for finding quantities
sumxi = sum(X);
sumyi = sum(Y);
sumxiyi = sum(X.*Y);
sumxi2 = sum(X.^2);
sumyi2 = sum(Y.^2);
%// Determine slope and intercept
m = (sumxi * sumyi - n*sumxiyi) / (sumxi^2 - n*sumxi2);
b = (sumxiyi * sumxi - sumyi * sumxi2) / (sumxi^2 - n*sumxi2);
%// Display them
disp([m b])
... and we get:
0.4250 0.7850
Therefore, the line of best fit that minimizes the error is:
y = 0.4250*x + 0.7850
However, if you want to use built-in MATLAB tools, you can use polyfit (credit goes to Luis Mendo for providing the hint). polyfit determines the line (or nth order polynomial curve rather...) of best fit by linear regression by minimizing the sum of squared errors between the best fit line and your data points. How you call the function is so:
coeff = polyfit(x,y,order);
x and y are the x and y points of your data while order determines the order of the line of best fit you want. As an example, order=1 means that the line is linear, order=2 means that the line is quadratic and so on. Essentially, polyfit fits a polynomial of order order given your data points. Given your problem, order=1. As such, given the data in the link, you would simply do:
X = 1:5;
Y = [1 2 1.3 3.75 2.25];
coeff = polyfit(X,Y,1)
coeff =
0.4250 0.7850
The way coeff works is that these are the coefficients of the regression line, starting from the highest order in decreasing value. As such, the above coeff variable means that the regression line was fitted as:
y = 0.4250*x + 0.7850
The first coefficient is the slope while the second coefficient is the intercept. You'll also see that this matches up with the link you provided.
If you want a visual representation, here's a plot of the data points as well as the regression line that best fits these points:
plot(X, Y, 'r.', X, polyval(coeff, X));
Here's the plot:
polyval takes an array of coefficients (usually produced by polyfit), and you provide a set of x co-ordinates and it calculates what the y values are given the values of x. Essentially, you are evaluating what the points are along the best fit line.
If you want to extend so that you're finding the best fit for any nth order polynomial, I won't go into the details, but it boils down to constructing the following linear system. Given the relationship for the ith point between (x_i, y_i):
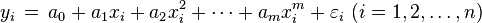
You would construct the following linear system:
Basically, you would create a vector of points y, and you would construct a matrix X such that each column denotes taking your vector of points x and applying a power operation to each column. Specifically, the first column is the zero-th power, the first column is the first power, the second column is the second power and so on. You would do this up until m, which is the order polynomial you want. The vector of e would be the residual error for each point in your set.
Specifically, the formulation of the problem can be written in matrix form as:
Once you construct this matrix, you would find the parameters by least-squares by calculating the pseudo-inverse. How the pseudo-inverse is derived, you can read it up on the Wikipedia article I linked to, but this is the basis for minimizing a system by least-squares. The pseudo-inverse is the backbone behind least-squares minimization. Specifically:
(X^{T}*X)^{-1}*X^{T} is the pseudo-inverse. X itself is a very popular matrix, which is known as the Vandermonde matrix and MATLAB has a command called vander to help you compute that matrix. A small note is that vander in MATLAB is returned in reverse order. The powers decrease from m-1 down to 0. If you want to have this reversed, you'd need to call fliplr on that output matrix. Also, you will need to append one more column at the end of it, which is the vector with all of its elements raised to the mth power.
I won't go into how you'd repeat your example for anything higher order than linear. I'm going to leave that to you as a learning exercise, but simply construct the vector y, the matrix X with vander, then find the parameters by applying the pseudo-inverse of X with the above to solve for your parameters.
Good luck!
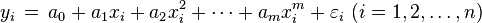
polyfit– Luis Mendo