Finding the smallest number of nodes that must be added to make a binary tree balanced?

Question

Suppose that you are given an arbitrary binary tree. We'll call the tree balanced if the following is true for all nodes:

1. That node is a leaf, or
2. The height of the left subtree and the height of the right subtree differ by at most ±1 and the left and right subtrees are themselves balanced.

Is there an efficient algorithm for determining the minimum number of nodes that need to be added to the tree in order to make it balanced? For simplicity, we'll assume that nodes can only be inserted as leaf nodes (like the way that a node is inserted into a binary search tree that does no rebalancing).

Answer 1

The following tree fits into your definition, although it doesn't seem very balanced to me:

EDIT This answer is wrong, but it has enough interesting stuff in it that I don't feel like deleting it yet. The algorithm produces a balanced tree, but not a minimal one. The number of nodes it adds is:

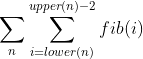
where n ranges over all nodes in the tree, lower(n) is the depth of the child of n with the lower depth and upper(n) is the depth of the child of n with the higher depth. Using the fact that the sum of the first k fibonacci numbers is fib(k+2)-1, we can replace the inner sum with fib(upper(n)) - fib(lower(n) + 2).

The formula is (more or less) derived from the following algorithm to add nodes to the tree, making it balanced (in python, only showing the relevant algorithms):

def balance(tree, label):
  if tree is None:
    return (None, 0)
  left, left_height = balance(tree.left_child, label)
  right, right_height = balance(tree.right_child, label)
  while left_height < right_height - 1:
    left = Node(label(), left, balanced_tree(left_height - 1, label))
    left_height += 1
  while right_height < left_height - 1:
    right = Node(label(), right, balanced_tree(right_height - 1, label))
    right_height += 1
  return (Node(tree.label, left, right), max(left_height, right_height) + 1)

def balanced_tree(depth, label):
  if depth <= 0:
    return None
  else:
    return Node(label(),
                balanced_tree(depth - 1, label),
                balanced_tree(depth - 2, label))

As requested: report the count instead of creating the tree:

def balance(tree):
  if tree is None:
    return (0, 0)
  left, left_height = balance(tree.left_child)
  right, right_height = balance(tree.right_child)
  while left_height < right_height - 1:
    left += balanced_tree(left_height - 1) + 1
    left_height += 1
  while right_height < left_height - 1:
    right += balanced_tree(right_height - 1) + 1
    right_height += 1
  return (left + right, max(left_height, right_height) + 1)

def balanced_tree(depth):
  if depth <= 0:
    return 0
  else:
    return (1 + balanced_tree(depth - 1)
              + balanced_tree(depth - 2))

Edit: Actually, I think that other than computing the size of a minimum balanced tree of depth n more efficiently (i.e. memoizing it, or used the closed form: it's just fibonacci(n+1)-1), that's probably as efficient as you can get, since you have to examine every node in the tree in order to test the balance condition, and that algorithm looks at every node precisely once.

Answer 2

Will this work?

Go recursively from the top. If the node A is imbalanced, add a node B on the short side and and enough left nodes to node B until node A is balanced.

(Of course, count the nodes added.)

Answer 3

First let's find the height of left child and right child of each node.

Now consider the root of the tree it's height is

1+max(height(root.left) , height(root.right)).

let's assume left has height of n-1 then right should have minimum height of n-2. Let's define another relation here req[node] -> the minimum required height of each node to make the tree balanced.

if you observe for a node to be at height h one of it's children should be at least at n-1 and to make it balanced the other children should be at at least n-2.

start from root with req[root] = height of root

The pseudo code is :

    def chk_nodes(root, req):

      if(root == NULL):
        return minNodes(req)

      if(left[root] > right[root]):
       return chk_nodes(root.left  , req-1) + chk_nodes(root.right , req-2)

      else return chk_nodes(root.left , req-2) + chk_nodes(root.right , req-1)

Now what is minNodes(int req)?

It's a function which return 'minimum no of nodes required to create a balanced binary tree of height h'. the function is quite intuitive and self-explanatory.

      def minNodes(int req) :
          if req < 0 : return 0
          return 1 + minNodes(req-1) + minNodes(req-2)

In minNodes function , a lookup table can be used to make it O(1) lookup time and O(N) for construction.

when the chk_nodes function runs recursively , at leaf-nodes we will be left with left-node , req . if that req > 0 then there should be a new sub-tree (balanced) with height req. Hence minNodes( req ) are required at this particular leaf-node.

With only 2 traversals and O(N) time, O(N) space the problem is solved.